报告地点:舜耕校区4号楼315会议室
报告时间:2025年11月30日(星期日)14:00—18:00
主办单位:山东财经大学统计与数学学院
协办单位:科研处,黄河流域生态统计协同创新中心、现代统计交叉科学重点实验室、统计学博士后科研流动站
一、青年教师工作论文报告
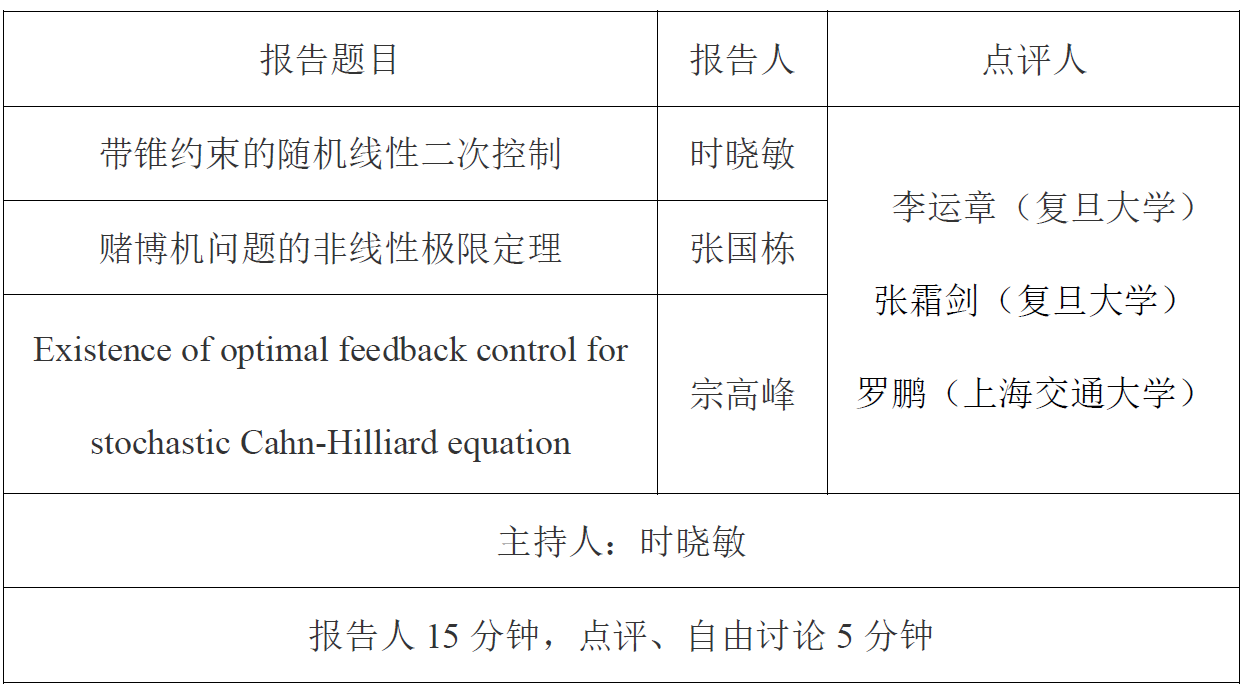
二、特邀专家报告
1. 报告题目:An Efficient Numerical Algorithm for BSPDEs Overcoming Curse of Dimensionality
报告人:李运章,复旦大学智能复杂体系基础理论与关键技术实验室
摘要:In this talk, we present an efficient numerical method for solving backward stochastic partial differential equations (BSPDEs), a class of problems notoriously challenging due to the curse of dimensionality because of spatial discretization. Our approach leverages a splitting technique to decompose the original BSPDE into simpler subproblems, overcoming the curse of dimensionality. The robustness result and optimal convergence rate of the algorithm are given for semi-linear BSPDEs. Numerical experiments are also provided to validate the theoretical results. This talk is based on a series of collaborative works with Juzhou Li, Jingtang Ma, Shanjian Tang, Yuyang Ye.
报告人简介:李运章,复旦大学智能复杂体系基础理论与关键技术实验室长聘副研究员、主任助理。主要研究领域为随机最优控制问题的高阶精度数值算法,相关成果发表于SIAM J. Control. Optim. (2篇), SIAM J. Sci. Comput., SIAM J. Financial Math., Stoch. Proc. Appl.等知名学术期刊。入选首批“启光学者”(全国共5名),上海市白玉兰人才计划浦江项目特殊急需类(人工智能方向),上海市晨光学者计划,国家博士后创新人才支持计划,上海市“超级博士后”激励计划。主持国家自然科学基金委青年科学基金项目,上海市“科技创新行动计划”基础研究领域项目,中国博士后科学基金面上项目,获得复旦大学新工科人才基金资助。
2.报告题目:Monopolist’s screening problem in 2D Rochet-Choné’s model
报告人:张霜剑,复旦大学数学科学学院
摘要:The monopolist problem is one of the central problems in microeconomics with many applications. Existence, uniqueness, convexity/concavity, regularity, and characterization of the solutions have been widely studied since 1970s. For multidimensional spaces of agents and products, Rochet and Choné (Econometrica, 1998) reformulated this problem to a concave maximization over the set of convex functions, by assuming agent preferences combine bilinearity in the product and agent parameters with a quasilinear sensitivity to prices. We characterize solutions to this problem by identifying a dual minimization problem. This duality allows us to reduce the solution of the square example of Rochet-Choné to a novel free boundary problem, giving the first analytical description of an overlooked market segment, where the regularity built by Caffarelli-Lions plays a crucial role —— an extension of their regularity work to the quasilinear case is also recently studied. In this talk, I will first introduce the historical work on the principal-agent framework under the context of the monopolist problem before moving to the recent progress. The results profoundly connect with the Optimal Transport theory, a powerful tool with potential applications in many areas. This talk contains my joint work with Robert J. McCann and Cale Rankin.
报告人简介:张霜剑,复旦大学数学科学学院青年研究员,博士生导师。2018年博士毕业于多伦多大学数学系;博士毕业后曾在巴黎高科国立统计与经济管理学院、巴黎高等师范学院、滑铁卢大学从事博士后研究。2023年9月至今任职于复旦大学数学科学院,研究方向为最优输运理论在经济金融中的应用,相关研究成果发表CPAM,MMMAS、Adv. Math.期刊上。曾入选国家级高层次青年人才计划。
3. 报告题目:Linear-quadratic extended mean field games with common noises
报告人:罗鹏,上海交通大学数学科学学院
摘要:We consider a class of linear quadratic extended mean field games (MFGs) with common noises where the state coefficients and the cost functional vary with the mean field term in a nonlinear way. Based on stochastic maximum principle, solving the mean field game is transformed into solving a conditional mean field forward-backward stochastic differential equation (FBSDE). We first establish solvability for a type of (more general) conditional mean field FBSDEs under monotonicity conditions. We further provide some regularity results which lead to classical solutions for the associated master equations. In particular, the linear quadratic extended mean field game is solved and classical solution for (extended mean field game) master equation is obtained.
报告人简介: 罗鹏,现为上海交通大学数学科学学院副教授,康斯坦茨大学和山东大学博士,苏黎世联邦理工学院和滑铁卢大学博士后。主要研究领域为随机分析、随机控制与金融数学,在SIFIN, JDE, SPA, EJP, AMO等期刊发表论文三十余篇, 主持和参与多项国家自然科学基金。

