报告地点:舜耕校区实验楼505
报告时间:2025年10月17日(星期五)9:00—12:00
主办单位:山东财经大学统计与数学学院
协办单位:科研处,黄河流域生态统计协同创新中心,现代统计交叉科学重点实验室,统计学博士后科研流动站
一、青年教师工作论文报告
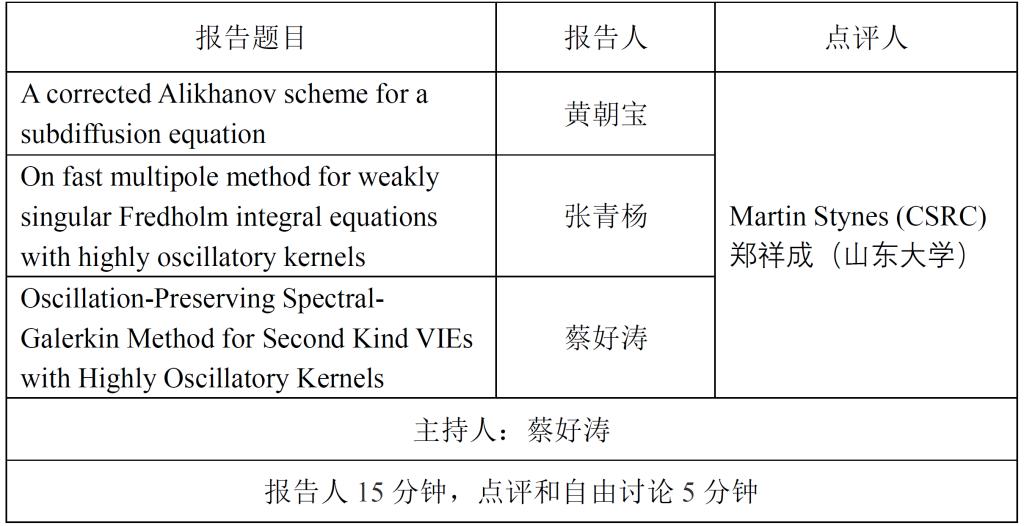
二、特邀专家报告
报告(一)
报告题目:Compatibility of collocation error analyses for Volterra integral equations with smooth and weakly singular kernels
报告人:Prof. Martin Stynes, Beijing Science Researcher Center
报告人简介:Martin Stynes obtained his B.Sc and M.Sc. degrees from University College Cork, Ireland, then his PhD degree from Oregon State University, USA in 1977. After some other positions, he was at University College Cork from 1984 to 2012. Since 2013 he has been at Beijing CSRC. He has worked for many years on the numerical solution of singularly perturbed differential equations; the book on this topic by Roos, Stynes and Tobiska is the standard international reference work (1st edition 1996, 2nd edition 2008). For the last 5 years he has worked mainly on fractional-derivative differential equations and their numerical solution. He is an editor of the journals Advances in Computational Mathematics, Journal of Scientific Computing, Fractional Calculus and Applied Analysis, and Computational Methods in Applied Mathematics.
报告摘要:The numerical solution by piecewise polynomial collocation and iterated collocation of Volterra integral equations (VIEs) of the second kind has been extensively studied and apparently sharp convergence results are known for the cases of a smooth kernel K(t,s) and a weakly singular kernel (t-s)^{-α}K(t,s), where α∈(0,1) is a parameter. If one takes the formal limit as α→0, then the weakly singular VIE reduces to the smooth VIE, but the known collocation error bounds for the weakly singular VIE do not become the collocation error bounds for the smooth VIE —— the error bounds for the smooth VIE are typically of a higher order. In the current paper this anomaly is explained and new sharper collocation and iterated collocation error bounds are derived for the weakly singular VIE that blend exactly as α→0 with known error bounds for the smooth VIE. This analysis is substantially different from previous VIE collocation analyses, e.g., it constructs a remarkable new decomposition of the solution of the weakly singular VIE, it investigates in detail the dependence on α of the matrices associated with collocation, it establishes a new Gronwall inequality, and the dependence of the error on the parameter α is traced precisely throughout the work.
报告(二)
报告题目:Multiscale solution decomposition of nonlocal-in-time problems with application in numerical computation
报告人:郑祥成研究员,山东大学
报告人简介:郑祥成,山东大学研究员、博士生导师,研究方向为非线性和非局部问题的分析与计算,相关成果发表在SIAM J. Numer. Anal.、SIAM J. Sci. Comput.、SIAM J. Control Optim.、Sci. China Math.等。主持国家自然科学基金青年项目C类、山东省自然科学基金青年项目B类、国家重点研发计划子课题等,入选中国工业与应用数学学会“青年人才托举工程”、山东省“泰山学者”青年专家、中国博士后国际交流计划引进项目、山东大学“齐鲁青年学者”,以主要完成人获山东省自然科学二等奖,担任中国工业与应用数学学会油水资源数值方法专业委员会副秘书长。
报告摘要:We develop a multiscale solution decomposition (MSD) method for nonlocal-in-time problems to separate a series of known terms with multiscale singularity from the original singular solution such that the remaining unknown part becomes smoother. We demonstrate that the MSD provides a scenario where the smoothness assumption for solutions of weakly singular nonlocal-in-time problems, a commonly encountered assumption in numerous literature of numerical methods that is in general not true for original solutions, becomes appropriate such that abundant numerical analysis results therein become applicable. From computational aspect, instead of handling solution singularity, the MSD significantly reduces the numerical difficulties by separating and thus circumventing the solution singularity. We consider typical problems, including the fractional relaxation equation, Volterra integral equation, subdiffusion, integrodifferential equation and diffusion-wave equation, to demonstrate the universality of MSD and its effectiveness in improving the numerical accuracy or stability in comparison with classical methods.

