报告地点:舜耕校区4号楼315会议室
报告时间:2025年6月7日(星期六)9:00—
主办单位:山东财经大学统计与数学学院
协办单位:科研处,黄河流域生态统计协同创新中心、现代统计交叉科学重点实验室、统计学博士后科研流动站
一、青年教师工作论文报告
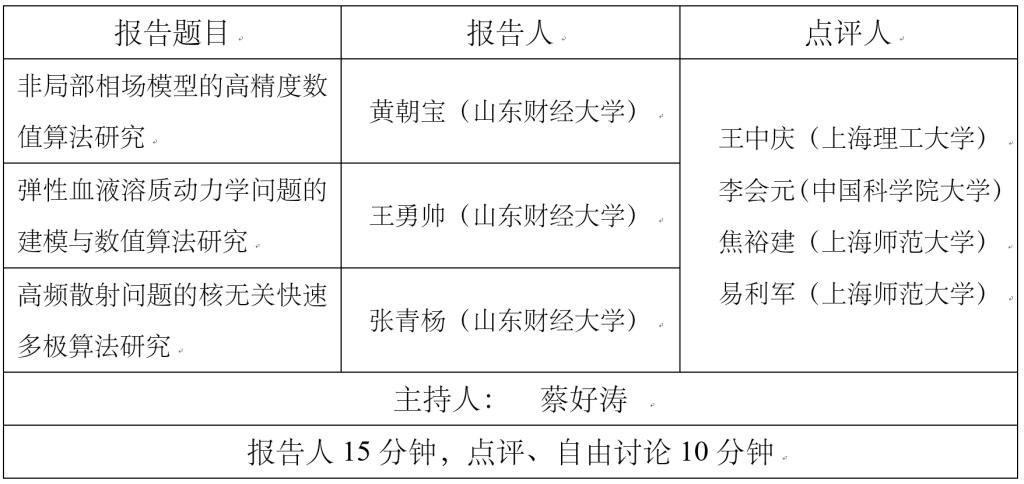
二、特邀专家报告
报告(一)
报告题目:An efficient spectral method for singularly perturbed convection-diffusion-reaction problems in three-dimensional irregular exterior domains
报告人:王中庆,教授(上海理工大学)
报告人简介:王中庆,上海理工大学教授、博士生导师,上海市曙光学者。长期从事偏微分方程数值方法的研究,在《Foundations of Computational Mathematics》、《SIAM Journal on Numerical Analysis》和《Mathematics of Computation》等学术期刊上发表论文100余篇。主持5项国家自然科学基金面上项目,获上海市自然科学二等奖。
摘要:This paper presents an efficient Fourier-Legendre-Jacobi rational spectral method, based on mapping techniques, for solving singularly perturbed convection-diffusion-reaction problems in a three-dimensional exterior domain with a complex obstacle. The solutions exhibit boundary or interior layer behavior as $\epsilon\rightarrow 0.$ The method begins by applying a spherical coordinate transformation to map the exterior domain of the complex obstacle onto the exterior of a unit sphere, while simultaneously transforming the convection-diffusion-reaction equation. The transformed equation is then formulated in its weak form, and a Fourier-Legendre-Jacobi rational spectral scheme is introduced. The paper provides a detailed description of the numerical implementation and analyzes the convergence of the solution in the $H^1$-norm. Numerical results demonstrate that the proposed method achieves high-order accuracy.
报告(二)
报告题目:Spectral Methods for the Transport Equation
报告人:李会元,研究员 (中国科学院大学)
报告人简介:李会元,中国科学院软件研究所研究员,博士生导师,并行软件与计算实验室常务副主任。主要从事偏微分方程谱方法、高性能软件与算法等研究工作,尤其是国产异构平台上高性能数值并行软件的研制与性能优化。先后在谱与谱元方法、非传统傅里叶变换与快速变换算法、高性能计算机基准测试、数学库研制、国产异构平台上高性能数值并行软件的研制与性能优化上取得了系列研究成果。现任中国数学会理事、CISAM谱方法及其应用专业委员会秘书,曾任中国系统仿真协会青年工作委员会委员、北京计算数学会理事。主持多项国家自然科学基金项目、参与多项国家自然科学基金委重点项目,承担多项国家重点研发计划高性能计算专项课题,承担华为基础数学库、HPC Benchmark及加速库系列项目;在SISC, JCP,SNIUM, MoC, TACO等国际国内高水平学术刊物上发表论文90余篇。
摘要:In this talk, we present some fully spectral approximation schemes for solving steady-state neutron transport equation. We utilize the spectral/spectral element scheme for the spatial approximation. While for the directional integral, we adopt specifically devised quadrature rules of Gauss-type or minimal cubature rules through spherical design. We furnish a rigorous proof of the solvability of these schemes and then conduct a comprehensive error analysis. Notably, the order of convergence is optimal both in directional dimensions and spatial dimensions. Finally, abundant numerical experiments are carried out to verify the computational efficiency and error characteristics of our schemes.
报告(三)
报告题目:Spectral Galerkin Methods Using Sinh Orthogonal Functions for Rapid Decay and Heavy-Tailed Problems
报告人:焦裕建,教授(上海师范大学)
报告人简介:焦裕建,博士,教授,博士生导师。从事偏微分方程数值解法(谱方法)研究,主要研究流体问题的高精度数值方法、分数阶微分方程的高精度数值方法等。主持项国家自然科学基金面上项目、上海市自然科学基金项目。在SIAM J. Numer. Anal., J. Comput. Phys., J. Sci. Comput., Appl. Numer. Math.,Appl. Math. Comput.等杂志发表论文。获上海市自然科学奖二等奖(第三)、上海市教学成果三等奖(独立)、上海市育才奖等奖项。
摘要:In this talk, we introduce a novel class of orthogonal functions, termed Sinh Orthogonal Functions (SOFs), derived from the inverse Sinh mapping. SOFs are designed to effectively tackle problems characterized by rapid decay or heavy-tailed distributions. These functions are mutually orthogonal in $L^2_{\omega}$, with the weight function $\omega(x)={\alpha}/{\sqrt{(\alpha x)^2+1}}$. A comprehensive theoretical framework is established to analyze the approximation properties of SOFs, highlighting the role of the parameter $\alpha$ in adjusting the distribution of Gauss nodes. Comparative studies with classical orthogonal bases, such as Hermite functions, scaled Hermite functions, and Rational orthogonal functions, reveal the superior efficiency of SOFs in approximating unbounded functions exhibiting exponential or algebraic decay. As practical applications, spectral Galerkin methods utilizing SOFs are developed for solving classical second-order differential equations and Burgers' equation. Both theoretical analysis and numerical experiments validate the effectiveness and computational efficiency of SOFs in addressing problems with rapid variations and heavy-tailed behaviors, demonstrating their broad applicability and robustness.
报告(四)
报告题目:Unified superconvergent postprocessing of Galerkin time-stepping methods for solving Volterra integro-differential equations
报告人:易利军,教授(上海师范大学)
报告人简介:易利军,上海师范大学数学系教授,博士生导师,主要从事积分和微分方程的高精度数值方法(尤其是谱方法和hp有限元方法)的理论及应用研究。先后主持多项国家级和省部级科研项目,获2023年度上海市自然科学奖二等奖(2/4);在《SIAM J. Numer. Anal.》、《Math. Comp.》、《Math. Models Methods Appl. Sci.》和《IMA J. Numer. Anal.》等国内外期刊发表论文50余篇。
摘要:In this talk I shall introduce a unified postprocessing technique of continuous and discontinuous Galerkin methods applied to solve first and second-order Volterra integro-differential equations. The core idea of this postprocessing technique is to augment the existing Galerkin approximation of degree $k$ with an additional term involving a generalized Jacobi polynomial (multiplied by appropriate coefficients) of degree $k+1$. The theoretical findings suggest that, through postprocessing, the convergence rate of the original Galerkin approximation error can be elevated by one order. Abundant numerical results underscore the effectiveness and high accuracy of the proposed postprocessing technique.

